Practical Class #07 - Binary Trees
(11/11 to 15/11)
Exercises for submission
In what concerns the continuous evaluation solving exercises during the semester, the exercises you can submit in this class are:
Submission Deadline: November 30th (submit to AED's Mooshak)
You are encouraged to talk to the professor and to your colleagues if you have difficulties. However, any more direct help you have received from other colleagues should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each class is worth 10 per cent of the grade for this component. As there will be 11 classes with submissions, you can get full marks even if you haven't done everything.
For a problem to count, you have to get all the tests right (i.e. accepted). Even if you solve all the problems, the maximum in a single class is 100 per cent.
it is guaranted that the main exercises on each class will sum to at least 100% of the class grade.
Lectures Content
This class is about binary trees implementation. It is therefore convenient that you know what was discussed on the lectures:
The exercises for this class will involve the low level implementation
of binary trees and adding new methods, so that you can gain a better understanding of trees and how they work, while at the same time training your algorithmic abilities.
On the following classes you will be allowed to use any STL classes that use trees as the underlying implementation (such as sets or maps), but for this class we want you to be able to understand (and code) an implementation. Moreover, C++ does not provide a built-in "vanilla" binary tree ready to be used.
1. Understanding Binary Trees
(the goal of this exercise is for you to understand what a binary tree is and some of the order in which we could traverse its nodes)
- Your first binary tree
One way of describing a tree is to use one of the following representations:
- preorder (DFS): root, followed by the preorder representation of the left subtree, followed by the preorder representation of the right subtree.
- inorder (DFS): inorder representation of the left subtree, followed by the root, followed by the inorder representation of the right subtree.
- postorder (DFS): postorder representation of the left subtree, followed by the postorder representation of the right subtree, followed by the root.
- breadth-first (BFS): nodes in increasing order of depth (from top to bottom) and on the same level from left to right
Consider of instance the tree of the following figure:
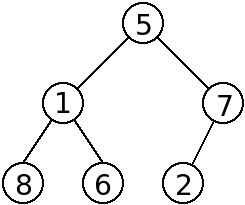
Using the 4 representation given before, the tree would be described as:
- preorder: 5 1 8 6 7 2
- inorder: 8 1 6 5 2 7
- postorder: 8 6 1 2 7 5
- breadth-first: 5 1 7 8 6 2
- Understanding traversal order.
To make sure you understood, write down the four representations given (preorder, inorder, postorder. breadth-first) but for the following tree:
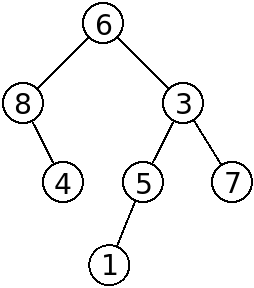
Solution
- preorder: 6 8 4 3 5 1 7
- inorder: 8 4 6 1 5 3 7
- postorder: 4 8 1 5 7 3 6
- breadth-first: 6 8 3 4 5 7 1
2. A binary tree implementation
(the goal of this exercise is for you to understand a basic implementation of binary trees that uses templates)
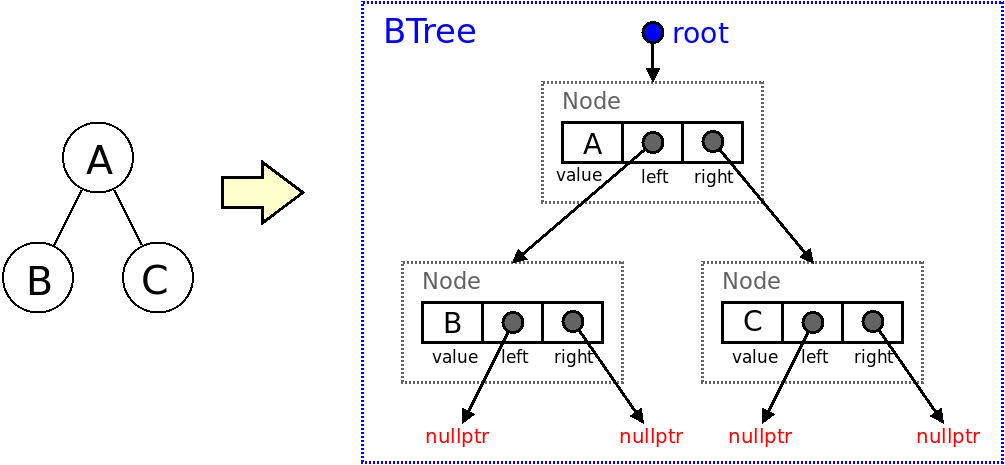
- Binary Trees - the code
Start by downloading the following two files: binaryTree.h (see it in html) and testBTrees.cpp (see it in html).
Compile the code. The whole BTree<T> class is contained in the .h file, so you just need to compile testBTrees.cpp (make sure they are in the same directory, so that the line #include "binaryTree.h" knows where to find the file it wants to include). If you are on a shell, you could for instance run g++ -std=c++17 -o testBTrees testBTrees.cpp to obain an executable with the name testBTrees).
- A first test
Download the file input.txt containing a line with 5 1 8 N N 6 N N 7 2 N N N. This is the preorder representation of the tree in the following figure, with N representing explicitely the nullptr nodes:
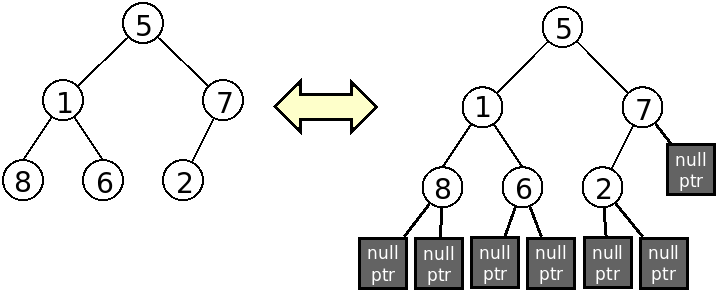
(the two representations in this figure refer to the same tree)
Now run the test code you compiled giving as input the file you downloaded (equivalent to writing its contents as the input):
./testBTrees < input.txt
You should obtain the following as the output:
numberNodes = 6
height = 2
contains(2) = 1
contains(3) = 0
PreOrder: 5 1 8 6 7 2
InOrder: 8 1 6 5 2 7
PostOrder: 8 6 1 2 7 5
BFS: 5 1 7 8 6 2
DFS: 5 7 2 1 6 8
Have a look at each method being called in binaryTree.h to understand how the binary tree is implemented. The figure above gives you an overview of how the class is organized and the class was shown and explained in the lectures.
- Templates and generalisation
Notice how the implementation uses templates to be general and therefore supports any data type (not just int).
To make sure you understand how to use it, create a file input2.txt that gives a preorder representation of the following tree ready to be read by the class, and give it as input to your program, testing if it gives the correct output.
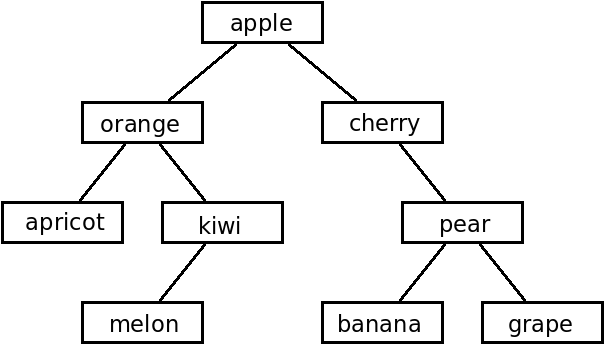
Solution
The file input2.txt should contain: apple orange apricot N N kiwi melon N N N cherry N pear banana N N grape N N
You can read this tree with the code:
BTree<std::string> t;
t.read("N");
If you are reusing the testBTrees.cpp file, notice that lines such as t.contains(2) will now give an error, because they should have as string as an argument (e.g. t.contains("orange"))
3. Your first binary tree method

For this exercise you will be solving the problem [AED032] Counting Leafs.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
For this practical class on all exercises except the last one (the challenge) you will be adding methods to an existing class, so the idea is that you add the requested method at the end of the class (but before the closing brackets). You only need to submit the binaryTree.h file!
If you want to test the method on your computer, you can copy+paste tester code from the problem statement to a file on your computer, compile it and use the input given to see if the results are as expected (note how easy it is to add new inputs, if you want to make further tests - you can simply give new trees with their preorder representation, as shown on the previous exercise).
This problems asks you to traverse the tree and count all leaves. Have a look at numberNodes(). What do you need to change to implement the numberLeafs method?
Hints
- The number of leaves in a tree is equal to the number of leaves in the left subtree plus the number of leaves in the right subtree
- A base case is when the current node is a leaf... in which case we should return 1
- Another base case is when the current is nullptr... in which case we should return 0
4. A boolean tree method

For this exercise you will be solving the problem [AED033] Strictly Binary Trees.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- A tree is strictly binary if BOTH its subtrees (left and right) are strictly binary.
- At each node, you must check if it is valid, i.e. if it is a leaf or if it has two children:
. If it's not valid, just return... false!
. If it is valid, you still need to check that BOTH the left and right subtrees are also strictly binary.
5. Processing Paths

For this exercise you will be solving the problem [AED034] Tree Paths.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- Besides the current node, your helper recursive method could have has arguments the path string s and the integer position pos where you are at the path
- Looking at s[pos], the current position in the path, we can decide if we should go to the left or to the right and recursively call the same method for the left or right node... but with the position incremented!
- The root case can be trated separately
6. Number of nodes at a certain depth

For this exercise you will be solving the problem [AED035] Deep Nodes.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- Can you do one exercise without any hints? 😉
Extra Exercises for Consolidating your knowledge [extra]
7. Counting Even Nodes

For this exercise you will be solving the problem [AED036] Even Nodes.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- This problem is simlar to counting the nodes or counting the leaves
- Instead of counting everything or just the leaves, count only the ones which are even (use the % operator to check for the remainder when divided by 2)
8. Sum of the nodes at a certain depth level

For this exercise you will be solving the problem [AED037] Sum of All Levels.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- Start by creating a vector with size equal to the height + 1 (note you already have a method for computing the height)
- While you are traversing the tree, if you keep track of which depth level you are, you can just sum the corresponding position in the vector (assuming you are also passing around a reference to the vector)
9. The path of maximum sum

For this exercise you will be solving the problem [AED038] Maximum Sum Path.
Desired time complexity: \(O(N)\) (where N is the number of nodes in the tree)
Hints
- One more without hints? 😉
Challenges Exercises [challenge]
The main idea of the challenge problems is to give you the opportunity of improving your problem solving abilities.

For this exercise you will be solving the problem [AED039] Recovering Lost Trees.
For this class, the problem is easier than the last one, but involves... trees! (of course 😁)
The input limits are small, so it is "just" about correctness.
Since this is a challenge, I will not give you any hints, but if you are stuck just contact @PedroRibeiro on Discord. Feel free to also contact @PedroRibeiro to discuss your accepted solution.
Happy coding! 😊




