In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of November 30th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #07 exercise sheet]
[AED039] Recovering Lost Trees
 A former professor of Algorithms and Data Structures had many examples of integer binary trees stored to show to his students. What he did was simply store the preorder and inorder representation of the trees (not indicating empty trees). As he always used different values in each node, this representation was enough to completely define the tree!
A former professor of Algorithms and Data Structures had many examples of integer binary trees stored to show to his students. What he did was simply store the preorder and inorder representation of the trees (not indicating empty trees). As he always used different values in each node, this representation was enough to completely define the tree!
Recall how to write a tree in preorder and inorder:
- preorder: root value, followed by the preorder representation of the left subtree, followed by the preorder representation of the right subtree.
- inorder : inorder representation of the left subtree, followed by the root value, followed by the inorder representation of the right subtree.
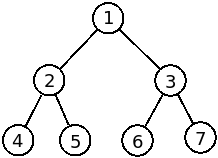
For instance, for the figure above, we have the following representations:
- preorder: 1 2 4 5 3 6 7
- inorder: 4 2 5 1 6 3 7
The new teacher of the subject wants to restore the trees and needs your help!
The Problem
Given the prerder and inorder representation of a binary tree your task is to reconstruct the tree. After that, you only need to show the postorder representation of the tree to show you were able to reconstruct it. Since the new professor is interested in knowing the number of leafs of the tree, you also need to compute it.
Recall how to write a tree in preorder and inorder:
- postorder: postorder representation of the left subtree, followed by the postorder representation of the right subtree, followed by the root value.
Input
The first input line contains an integer T, indicating the number of trees to consider.
Each tree is indicated by three lines:
- the first line contains N, the number of nodes in the tree
- the second line contains the preorder representation of the tree (N space separated integers)
- the third line contains the inorder representation of the tree (N space separated integers)
You can assume all the integer values of the same tree will be different and will fit on a normal int type.
Output
For each tree in the input the output should be:
- a first line with the postorder representation of the tree (N space separated integers)
- a second line containing "leafs = L" where L is the number of leafs in the tree
Note that there there should be a single space between the numbers of the postorder representation (and no space after the last number)
Constraints
The following limits are guaranteed in all the test cases that will be given to your program:
| 1 ≤ T ≤ 5 |
|
Number of trees in the input |
| 1 ≤ N ≤ 50 |
|
Number of nodes in one tree |
| Example Input |
Example Output |
4
7
1 2 4 5 3 6 7
4 2 5 1 6 3 7
3
1 2 3
1 2 3
3
1 2 3
2 1 3
3
1 2 3
3 2 1
|
4 5 2 6 7 3 1
leafs = 4
3 2 1
leafs = 1
2 3 1
leafs = 2
3 2 1
leafs = 1
|
Algorithms and Data Structures (L.EIC011) 2024/2025
DCC/FCUP & DEI/FEUP - University of Porto
 A former professor of Algorithms and Data Structures had many examples of integer binary trees stored to show to his students. What he did was simply store the preorder and inorder representation of the trees (not indicating empty trees). As he always used different values in each node, this representation was enough to completely define the tree!
A former professor of Algorithms and Data Structures had many examples of integer binary trees stored to show to his students. What he did was simply store the preorder and inorder representation of the trees (not indicating empty trees). As he always used different values in each node, this representation was enough to completely define the tree!
