In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of December 14th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #09 exercise sheet]

[AED055] Bipartite Graphs

In this problem you should only submit a graph.h file with a self-containing definition of a class Graph.

Base Code

Use as a basis the class Graph (see code | download code) which implements a graph (that can have directions and weights) using an adjacency list, assumes nodes are identified by integers between 1 and |V| and already has methods for adding an edge, reading a graph and doing a basic DFS and a basic BFS.

The Problem

Add a new method bool isBipartite() to the class. If called on an undirected graph, the function should return true of the graph has is bipartite or false otherwise. A graph is bipartite if its nodes can be divided into two distinct node sets, such that no edges connect nodes within the same set.

All the input graphs will be simple (no self-loops or parallel edges), unweighted, undirected and connected (that is, they will have a single connected component). It is guaranteed that |V|<=100 and |E|<=500.

Submission

You should submit the file graph.h with the method isBipartite added to Graph as requested (and without removing any of the other existing methods). You can however create additional methods and/or attribute variables, if you need them.

Mooshak will use the following code to link to your class, read the inputs, build the graphs and call your method, printing its result.

#include <iostream>
#include <list>
#include "graph.h"

int main() {

  // Number of graphs to test
  int n;
  std::cin >> n;

  // For each graph: read, call the method and delete graph at the end
  for (int i=1; i<=n; i++) {
    Graph *g = Graph::readGraph();
    std::cout << "Graph #" << i << ": isBipartite() = " << (g->isBipartite()?"true":"false") << std::endl;
    delete g;
  }
    
  return 0;
}

4

8 undirected unweighted
9
1 2
2 3
3 4
1 5
1 6
3 6
3 7
4 8
7 8


8 undirected unweighted
10
1 2
2 3
3 4
1 5
1 6
3 6
3 7
4 8
7 8
6 7

7 undirected unweighted
8
1 2
2 3
3 4
1 5
3 6
4 7
5 6
6 7

7 undirected unweighted
6
1 5
2 5
2 6
3 6
4 6
4 7

Graph #1: isBipartite() = true
Graph #2: isBipartite() = false
Graph #3: isBipartite() = false
Graph #4: isBipartite() = true

Explanation of Example Input

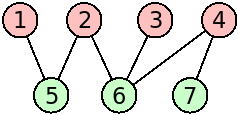
The first graph of the example input corresponds to the following figure:
(which is bipartite - consider the two sets of nodes indicated on red and green with no links between nodes of the same color):

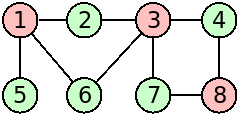
The second graph of the example input corresponds to the following figure:
(it is not bipartite):

The third graph of the example input corresponds to the following figure:
(it is not bipartite)

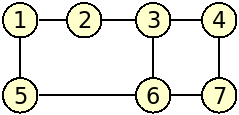
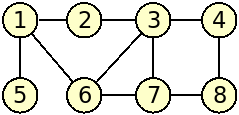
The fourth graph of the example input corresponds to the following figure:
(which is bipartite - consider the two sets of nodes indicated on red and green with no links between nodes of the same color):