Practical Class #09 - Introduction to Graphs + DFS
(25/11 to 29/11)
Exercises for submission
In what concerns the continuous evaluation solving exercises during the semester, the exercises you can submit in this class are:
Submission Deadline: December 14th (submit to AED's Mooshak)
You are encouraged to talk to the professor and to your colleagues if you have difficulties. However, any more direct help you have received from other colleagues should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each class is worth 10 per cent of the grade for this component. As there will be 11 classes with submissions, you can get full marks even if you haven't done everything.
For a problem to count, you have to get all the tests right (i.e. accepted). Even if you solve all the problems, the maximum in a single class is 100 per cent.
it is guaranted that the main exercises on each class will sum to at least 100% of the class grade.
Lectures Content
This class is about graphs and essential usages of DFS. It is therefore convenient that you know what was discussed on the lectures:
The exercises for this class will involve the implementation of graphs and adding new methods to add functionality (there is no available implementation of graphs in the C++ standard). You will also have some exercises where the graph is not explicit.
1. A graph implementation
(the goal of this exercise is for you to understand the simple and lightweight graph implementation that was discussed on the lectures)
- Graph - the code
Start by downloading the following two files: graph.h (see it in html) and testGraphs.cpp (see it in html).
Compile the code. The whole Graph class is contained in the .h file, so you just need to compile testGraph.cpp (make sure they are in the same directory, so that the line #include "graph.h" knows where to find the file it wants to include). If you are on a shell, you could for instance run g++ -std=c++17 -o testGraphs testGraphs.cpp to obtain an executable with the name testGraphs).
Have a look at the code in graph.h to understand how the graph is stored (using an adjacency list)
- The graph itself has 3 main attributes:
- int n (number of nodes, which are are numbered from 1 to n)
- bool hasDir (true if the graph is directed, false otherwise)
- std::vector<Node> nodes (the nodes in the graph)
- Each node is represented by a struct that contains 2 attributes:
- std::list<Edge> adj; (the list of outgoing edges to adjacent nodes)
- bool visited (to indicate if the nodes has been visited on a graph traversal)
- Each edge is represented by a struct that contains 2 attributes:
- int dest (the destination node)
- int weight (the weight of that edge)
- A first test
Download the file input_graph.txt the representation of a graph that you can be read by calling the static Graph::readGraph() method:
Calling Graph::readGraph()
and giving the following as input: |
|
Is "equivalent" to the the following code: |
|
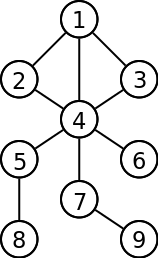
Which corresponds to
the following graph: |
9 undirected unweighted
10
1 2
1 3
1 4
2 4
3 4
4 5
4 6
4 7
5 8
7 9
|
|
Graph g(9, false); // create an undirected graph with 9 nodes
g.addEdge(1, 2); // assuming weight=1 (unweighted)
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 4);
g.addEdge(3, 4);
g.addEdge(4, 5);
g.addEdge(4, 6);
g.addEdge(4, 7);
g.addEdge(5, 8);
g.addEdge(7, 9);
|
|
|
Now run the test code you compiled giving as input the file you downloaded (equivalent to writing its contents as the input):
./testGraphs < input_graph.txt
You should obtain the following as the output:
DFS: 1 2 4 3 5 8 6 7 9
BFS: 1 2 3 4 5 6 7 8 9
Have a look at each method being called in graph.h to understand how the graph is implemented. For now you should just understand completely the constructor, addEdge and readGraph (which is a static function). DFS will be further explored on other exercises in the class and BFS will be explored on the next class (but is already give so that you already have the full graph class that will be used in this course.
2. Your first mooshak exercise with graphs

For this exercise you will be solving the problem [AED049] Node Degree.
Desired time complexity: \(O(1)\)
For this practical class on all exercises except the last two you will be adding methods to an existing class, so the idea is that you add the requested method at the end of the class (but before the closing brackets). You only need to submit the graph.h file!
If you want to test the method on your computer, you can copy+paste tester code from the problem statement to a file on your computer, compile it and use the input given to see if the results are as expected (note how easy it is to add new inputs, if you want to make further tests - you can simply give new graphs in the format shown before).
This problems asks you to return the number of outgoing edges of a node v and is essentially asking if you understood the graph data structure (it is as simple as it gets!).
Hints
- You just need to return... the size of the adjacency list of node v
- This can be easily done by simply returning nodes[v].adj.size()
3. Traversing the edges of a node

For this exercise you will be solving the problem [AED050] Weighted Node Degree.
Desired time complexity: \(O(degree(v))\) (where v is the node for which you are computing the weighted degree)
Here you just need to traverse the ougoing edges and summing their weights, showing you know how to traverse the adjacency list 🙂
Hints
- You just need to traverse nodes[v].adj.size(), which is a list of edges
- Notice that each edge has two attributes and you want to sum only the weight
4. Your first exercise with DFS in a graph

For this exercise you will be solving the problem [AED051] Number of Connected Components.
Desired time complexity: \(O(|V| + |E|)\) (where V is the set of nodes and E is the set of edges)
This is exercise is directly explained (and implemented) in the lecture slides: 11 - Graphs: Depth-First Search (DFS) [slides 11 to 15]
If you want you can have a look at a DFS visualization.
Hints
- The solutions is essentially in slide 15. Can you understand it?
- Each time you start a new dfs, you are on a new component and you visit all the nodes of that component
5. Counting nodes in a component

For this exercise you will be solving the problem [AED052] Largest Component.
Desired time complexity: \(O(|V| + |E|)\) (where V is the set of nodes and E is the set of edges)
Here you need to show you understood the previous code. If yes, than this is pretty easy, right?
Hints
- You can for instance modify your dfs (or create a new one) that returns the number of visited nodes
- To implement this, you can do like in trees: you just add 1 + the node count of all recursive dfs calls
- After having this function, you just need to keep the largest size and update it after visiting each component
6. Topological Sorting

For this exercise you will be solving the problem [AED053] Topological Sorting.
Desired time complexity: \(O(|V| + |E|)\) (where V is the set of nodes and E is the set of edges)
This exercise asks you to understand the order of DFS and use it in your advantage.
A possible solution is directly explained in the lecture slides: 11 - Graphs: Depth-First Search (DFS) [slides 17 to 19].
Do you understand why it works? Can you implement the idea in C++ and using the graph class provided? Have a look at a possible visualization.
As an extra curiosity, this exercise uses a special corrector in Mooshak: instead of simply comparing your output with the "official output", it really reads it an checks if it is a valid topological sorting. 🙂
Although our suggestion is for you to implement the idea given in the slides, there are other possible algorithms for this task. For instance, the initial nodes need to be the ones with indegree equal to zero, right? And after that which ones should come? (if you try this idea, try to think about the associated time complexity).
Hints
- You can for instance modify your dfs (or create a new one) to receive an extra argument: the order you are building (passed as a reference)
- The order can be the asked list<int>
- When leaving a dfs recursive call you can simply use push_front to put it on the fron of the order (you know that everything called within the dfs is necessarily a descendant and therefore should appear afterwards in the order)
7. Detecting Cycles

For this exercise you will be solving the problem [AED054] Cycle Detection.
Desired time complexity: \(O(|V| + |E|)\) (where V is the set of nodes and E is the set of edges)
A possible solution is directly explained in the lecture slides: 11 - Graphs: Depth-First Search (DFS) [slides 20 to 23].
Do you understand why it works? Can you implement the idea in C++ and using the graph class provided?
Hints
- You can add a new attribute to the node struct, indicating the color (it can be for instant an int)
- You can then use the color on your dfs for this problem as explained in the slides
Extra Exercises for Consolidating your knowledge [extra]
8. Seeing if a graph is bipartite

For this exercise you will be solving the problem [AED055] Bipartite Graphs.
Desired time complexity: \(O(|V| + |E|)\) (where V is the set of nodes and E is the set of edges)
One exercise without help from the slides but that can be solved with DFS. Can you solve it? The hints provide an algorithm, but try first to think a bit about the problem by yourself.
Hints
- A possible algorithm would be the following:
. Start a dfs on node v and paint that node with color c
. for each neighbor node w of v, if not visited recursively call dfs(w) and paint with color different than c
. if w was already visited, check if color was the same as c: is yes, than graph cannot be bipartite
. if we visit all nodes without any counterexample (two connected nodes of the same color) than the graph is bipartite
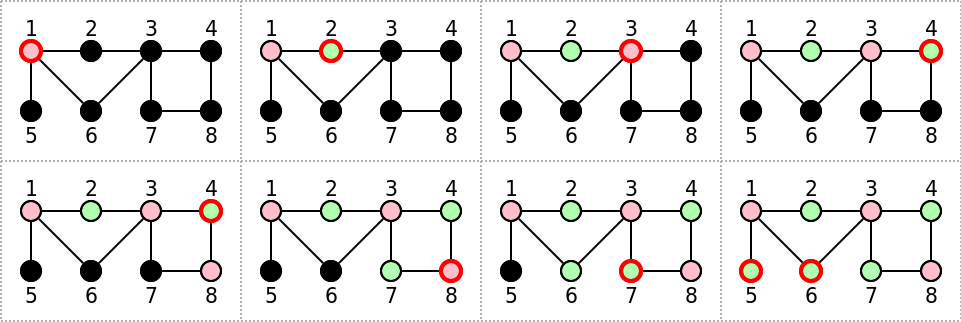
- Here is a visualization of this algorithm working on the first graph of the input (which is bipartite):
. we start with dfs(1) and paint the node as "red" (set A)
* this implies that to be bipartite, all its neighbors (2, 5 and 6) must be "green" (set B)
. we initiate recursive calls to its neigbors and we start we dfs(2) painting it as "green"
* this implies that to be bipartite, all its neighbors (1 and 3) must be "red"
. (..)
. At the end we conclude that the graph is bipartite with sets A={1,3,8} and B={2,4,5,6,7}
9. DFS on a 2D grid - an implicit graph

For this exercise you will be solving the problem [AED056] Counting Cells.
Desired time complexity: \(O(R \times C)\) (where R is the number of columns and C the number of columns of the grid)
This is really just a graph problem asking for... the number of connected components and the size of the largest component 😉
The difference is that now the graph is not explicit, but it is the same as saying that:
- The nodes are the positions of the grid
- Each cell is adjacent to the 8 positions around it
To solve this problem you can either:
- Explicitly create graph and solve it after that), or
- Solve directly on the grid
We suggest to solve directly on the grid, adapting your code correspondently (if you use the graph, remember to submit only a single .cpp file to Mooshak - you can just put the Graph code inside the submitted file)
Hints
- Doing a DFS like this on a 2D grid is known as doing a Flood Fill
- Can you do one exercise without more hints?
Challenges Exercises [challenge]
The main idea of the challenge problems is to give you the opportunity of improving your problem solving abilities.

For this exercise you will be solving the problem [AED057] Slash Maze.
For this class, the problem is easier than the last one, but involves... graphs! (of course 😁)
The main difficulty is that the graph itself is more complex and less easy to represent.
Since this is a challenge, I will not give you any hints, but if you are stuck just contact @PedroRibeiro on Discord. Feel free to also contact @PedroRibeiro to discuss your accepted solution.
Happy coding! 😊

