Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 10 17 de maio
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #07]

[DAA 025] Redes de circuitos electrónicos

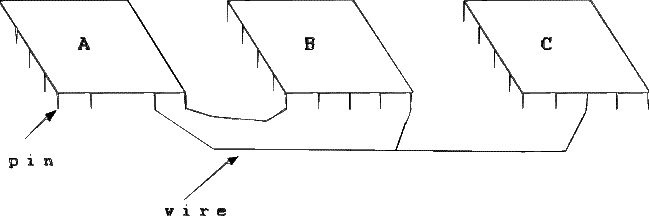
Um circuito electrónico consiste em diversos componentes, pontos de contacto (pins) e ligações (wires). A figura seguinte mostra um circuito com 3 componentes: A, B e C. Cada ligação envolve um par de pontos de contacto.

Dois pontos de contacto a e b dizem-se electronicamente equivalentes se têm uma ligação directa entre eles, ou se se existe um sequência de pontos de contacto a₁, a₂, ..., a_k, tal que existe ligação entre (a,a₁), (a₁,a₂), ..., (a_k, b). Uma rede é um conjunto máximo de pontos de contacto electronicamente equivalentes. Máximo é aqui usado no sentido de traduzir que nenhum ponto de contacto fora da rede é electronicamente equivalente a qualquer ponto dentro da rede.

O Problema

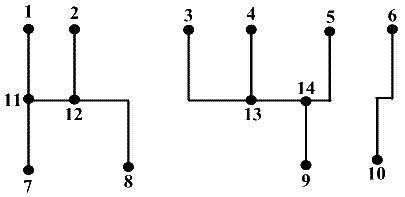
Dado um conjunto de pontos de contacto e as suas respectivas ligações, a tua tarefa é descobrir o número de redes diferentes que existem no circuito. A figura seguinte ilustra um circuito com 3 redes.

Input

Na primeira linha vem um número N indicando o número de pontos de contacto existentes. Na segunda linha vem um número L indicando o número de ligações existentes. Seguem-se L linhas, cada uma com um par de números diferentes indicando que pontos de contacto estão conectados pela ligação. Os pontos de contacto são sempre identificados por números de 1 até N. Note que as ligações não vêm por nenhuma ordem em específico e que nunca aparecem ligações repetidas.

Output

Deve ser imprimida uma única linha, contendo o número de redes do respectivo circuito.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Exemplo de Input

14
11
1 11
7 11
11 12
12 2
12 8
3 13
13 4
13 14
14 9
14 5
10 6

Exemplo de Output

3

Explicação do Input/Output

O exemplo de input corresponde à figura do enunciado.

Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto