Aula Prática #07 - Introdução a Grafos e Pesquisa em Profundidade
(aulas de 20/04 e 24/04)
Exercícios para submissão
Para efeitos da nota atribuída à resolução de exercícios ao longo do semestre, os exercícios a submeter desta aula são:
Prazo de submissão: 10 17 de maio (submeter no Mooshak de DAA)
Não se esqueçam que qualquer ajuda que tenham recebido de outros colegas deve ser reconhecida nos comentário do programa que submetem.
Depois do prazo os problemas continuarão disponíveis no Mooshak, mas as submissões não contarão para a sua nota. Relebre que cada aula vale 10% da nota desta componente.
Para um problema contar tem acertar todos os testes. Mesmo que resolva todos os problemas, o máximo numa aula é de 100%.
Conteúdos das teóricas
Nesta aula iremos abordar conceitos de Grafos. Será por isso conveniente ver o que foi falado nas teóricas:
- Slides (capítulos "6 - Grafos: Introdução" e primeira parte de "7 - Grafos: Pesquisa)
- Vídeos: (vídeos #16 e #17)
Exercício 1) Introdução à pesquisa em profundidade (DFS)
Comece por fazer download do código exemplo de pesquisa em profundidade:
- O código usa matriz ou lista de adjacências?
- Considere o seguinte grafo não dirigido:
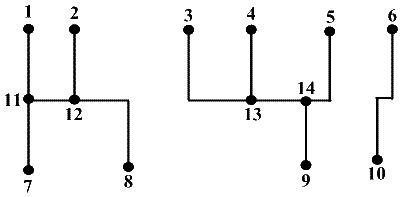
Uma maneira de o representar é através de um ficheiro no seguinte formato (na primeira linha vem o número de nós, na segunda o número de arestas e depois vêm as arestas em si):
14
11
1 11
7 11
11 12
12 2
12 8
3 13
13 4
13 14
14 9
14 5
10 6
Copie esta representação para um ficheiro e execute a pesquisa em profundidade exemplo para este grafo redirecionando o input. O que é imprimido? Consegue perceber a ordem em que os nós são imprimidos?
- O que acontece se mudar a linha dfs(1) para dfs(3)?
- Como poderia visitar todo o grafo ao invés de uma só componente conexa?
Exercício 2) Problema com DFS I - contando componentes conexas

Implemente e submeta uma solução para o problema [DAA 025] - Redes de circuitos electrónicos.
Dicas:
- Basicamente o problema pede-lhe para contar o número de componentes conexos
- Pode usar como base o código exemplo anterior, bastando:
- Fazer DFS a partir de cada nó não visitado
- Incrementar um contador de cada vez que começa um novo DFS
- No final imprimir o contador
- Este algoritmo está nos slides das teóricas [ver slides 9 e 10 do "capítulo 7 - Grafos: Pesquisa"]
Exercício 3) Problema com DFS II - a maior componente conexa

Implemente e submeta uma solução para o problema [DAA 026] - Contagem de células.
Dicas:
- Basicamente o problema pede-lhe para descobrir o maior componente conexo
- É essencialmente um exercício igual ao anterior, bastando que:
- Dentro do DFS, cada vez que entre num novo nó incremente um contador
- Cada vez que sai de um componente conexo, verificar se o tamanho é maior do que o actual máximo
- No final imprimir o máximo global
- Não é necessário criar explicitamente o grafo. Basta guardar a matriz e depois o grafo fica implícito. Em particular, para a posição (x,y), em que posições estão os 8 "nós" vizinhos? [ver slide 11 do "capítulo 7 - Grafos: Pesquisa"] (notar que para este problema as posições adjacentes na diagonal também são vizinhas)
Exercício 4) Problema com DFS III - grafos bipartidos

Implemente e submeta uma solução para o problema [DAA 027] - Grafos bipartidos.
Dicas: use o algoritmo explicado nos slides [ver slides 12 a 15 do "capítulo 7 - Grafos: Pesquisa"]
Exercício de Desafio
Todas as semanas vou colocar disponível pelo menos mais um exercício um pouco mais desafiante.
Para esta semana o desafio tem mais a ver com como codificar e implementar o grafo, e não é especialmente complicado do ponto de vista da eficiência temporal. O problema está disponível para submissão no Mooshak:
Se já tiverem feito tudo e estiverem "presos" neste, e quiserem mesmo fazer o desafio, podem contactar-me para eu "dosear" as dicas.

