Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 10 17 de maio
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #07]

[DAA 028] Labirinto de barras
(este problema é essencialmente uma tradução/adaptação de um problema do UVA Online Judge)

Já reparaste que se pegares num rectângulo e o encheres com barras ("\" e "/") consegues criar um labirinto muito engraçado?

Repara na seguinte figura:

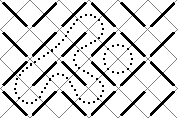
Como podes ver, caminhos em labirintos como este não podem ter ramificações (dividirem-se em dois ou mais ramos) e como tal todos os caminhos dentro do labirinto só podem ser cíclicos ou então começarem num sítio e acabarem noutro.

Neste problema estamos apenas interessados nos caminhos cíclicos. Recorda que um caminho é cíclico se for possível começar num ponto e voltar a ele mesmo através desse caminho.

O Problema

A tua tarefa é escrever um programa para contar os ciclos e descobrir qual o maior deles. O tamanho de um ciclo é definido como o número de pequenos quadrados (os que estão delimitados na figura por traços cinzentos) que o ciclo contém. Por exemplo, na figura, temos dois ciclos, um com tamanho 16 e outro com tamanho 4.

Input

Na primeira linha vêm dois números inteiros, C e L, indicando respectivamente o número de colunas e de linhas do labirinto.

Seguem-se L linhas, indicando o formato do labirinto (tal como descrito anteriormente), sendo que cada linha contém exactamente C caracteres, que só podem ser "\" ou "/".

Não te esqueças de verificar o exemplo de input para perceberes melhor a especificação (o primeiro exemplo de input corresponde à figura).

Output

Se o labirinto não tiver nenhum caminho cíclico, deve ser impressa a frase "nao tem ciclos". Caso contrário, deve ser impresso "NUM_CICLOS MAIOR_TAM", onde NUM_CICLOS é o número total de ciclos e MAIOR_TAM o tamanho do maior ciclo.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Exemplo de Input 1

6 4
\//\\/
\///\/
//\\/\
\/\///

Exemplo de Output 1

2 16

Exemplo de Input 2

3 3
///
\//
\\\

Exemplo de Output 2

nao tem ciclos

Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto